While loops
In addition to for loops which run for a set number of iterations, Python has another type of loop. while loops iterate until a particular condition is met.
What is a While Loop?
Conditions
While loops use conditions just like if statements. A while loop takes a boolean
expression and evaluates the expression every time it is about to start another loop.
If the expression is True, the loop runs again. This is useful in situations where
a process might need to run a bunch of times. In the example below, we ask the
user to give us a number between one and ten. The user might do this in the first try,
or it might take a few tries if they are ornery.
user_input = -1
while user_input < 1 and user_input > 10:
user_input = int(input("Tell me a number between 1-10 (inclusive): "))
print("Thanks.")
While True / Break
What if you wanted a loop to run forever? You could use an expression which is always True,
like 1 + 1 == 2, but a simpler expression which is always True is simply True.
To stop a loop like this, you can use a break statement. Once the program reaches the
break, it will break out of the loop and continue with the rest of the program.
You’ve actually already seen an example of this kind of loop when you learned about
conditionals in the previous lab.
speed(10)
while True:
drawing = input("What would you like me to draw? ")
size = int(input("How big should I draw it? "))
if drawing == "square":
for i in range(4):
forward(size)
right(90)
elif drawing == "quit":
break
else:
print("Sorry, I don't know how to draw that...")
Hailstone Sequence
Calculate the sequence
In the first part of this lab, you will be exploring a special sequence known as the hailstone sequence.
This sequence results from the following rules (known as the Collatz conjecture):
- take any positive number
n - find the next term of the sequence using the following rules:
- if
nis even, the next term isn/2 - if
nis odd, the next term isn*3+1
- if
- repeat until
n == 1
The conjecture states that no matter the starting value of n, the sequences will always reach 1.
For example, if you started with n=10, the sequence would be 10, 5, 16, 8, 4, 2, 1. It took six
steps to reach n == 1.
✅ CHECKPOINT:
In your notebook, pick a number and perform the calculations. Can you find a number that doesn’t reach 1? If you do, immediately contact your nearest mathematician. No number has ever been found that doesn’t reach 1, but nobody has been able to prove that there isn’t such a number.
Plan
Before you start programming, write out pseudocode to think through how the program will work. Your program should:
- Ask the user what number the program should calculate the hailstone sequence of.
- Print out each number in the sequence.
- Print out how many steps it took for the sequence to reach
1
Here are some things to consider:
- This program will require a loop. What kind of loop do you think is best? Remember that for loops run for a definite number of times and while loops run until a condition is met.
- You will need to determine if each term is odd or even. What are some characteristics of even numbers that will help you determine if a number is even?
- In addition to calculating each term, you must count how many steps it takes to reach 1 and report this number at the end.
✅ CHECKPOINT:
Write out pseudocode to plan the logic of this program.
Code
💻 Write your program
in ~/Desktop/making_with_code/pedprog/unit00/lab05/hailstone_sequence.py.
✅ CHECKPOINT:
Answer the following check-in questions on your notebook before moving on:
- What kind of loop did you choose to write the hailstone sequence algorithm? Why did you choose this kind of loop?
- Describe a moment when your code didn’t do what you intended. How did you fix it?
- Why do you think the Collatz conjecture is so hard to prove for all positive integers?
Extension
Visualize the sequence
The sequences formed are known as hailstone sequences, because the terms move up and down but ultimately reach 1. Similarly, hailstones rise and fall within a cloud, gradually gaining layers of ice until they finally fall to the ground.
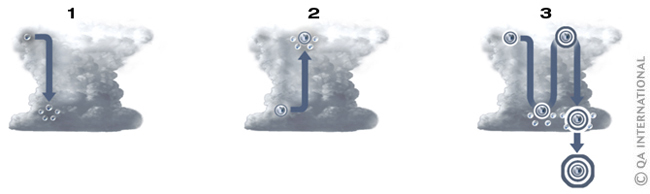
Hailstones forming in a cloud
This pattern can lead to some interesting visualizations of hailstone sequences.
💻 Use your hailstone sequence code to create a visualization for the hailstone sequence using Turtle.You can visualize the terms in a sequence starting with a specific number:
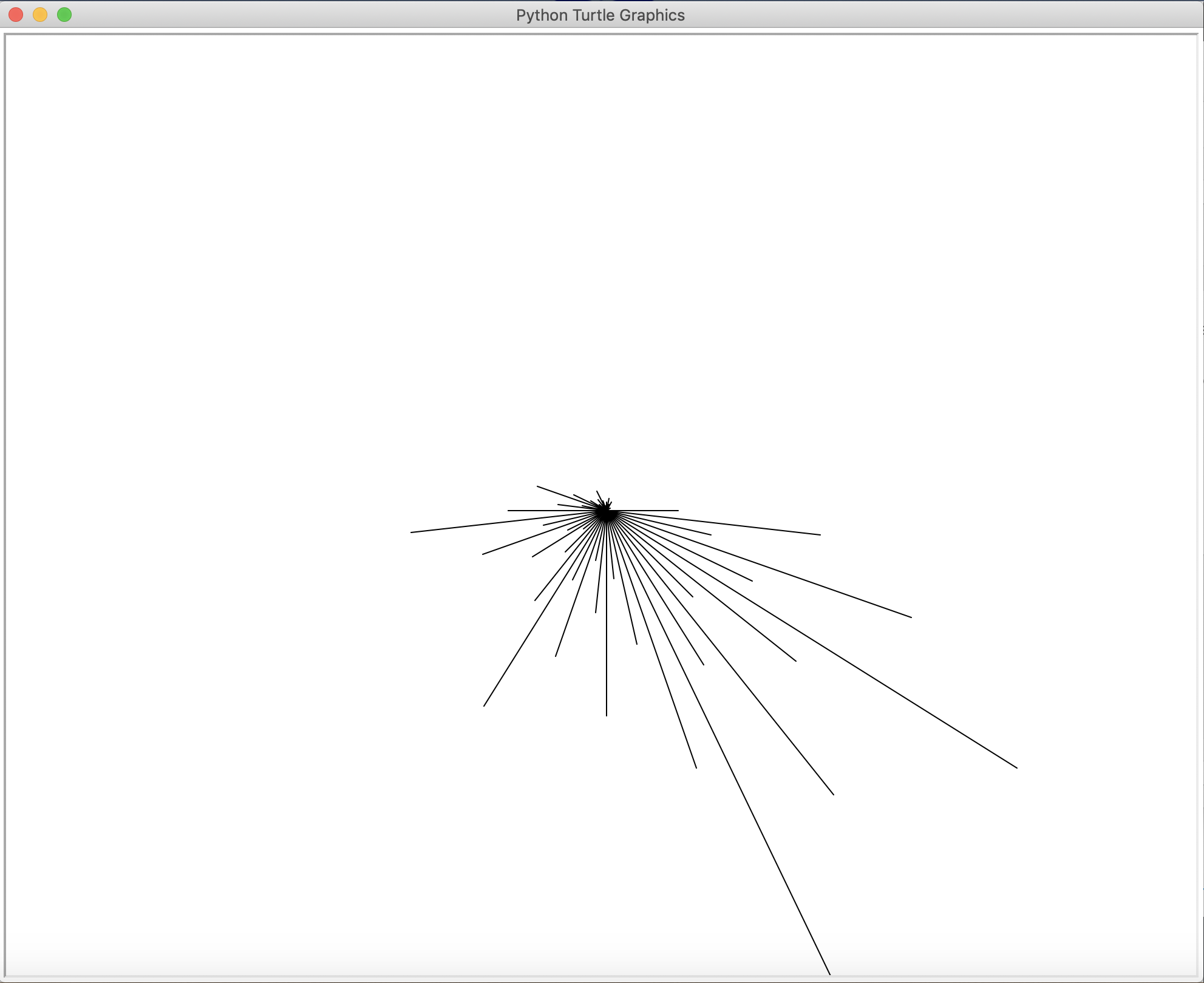
Terms in hailstone sequence starting at 590
Or you can visualize the number of steps it takes to reach one from a set of integers:
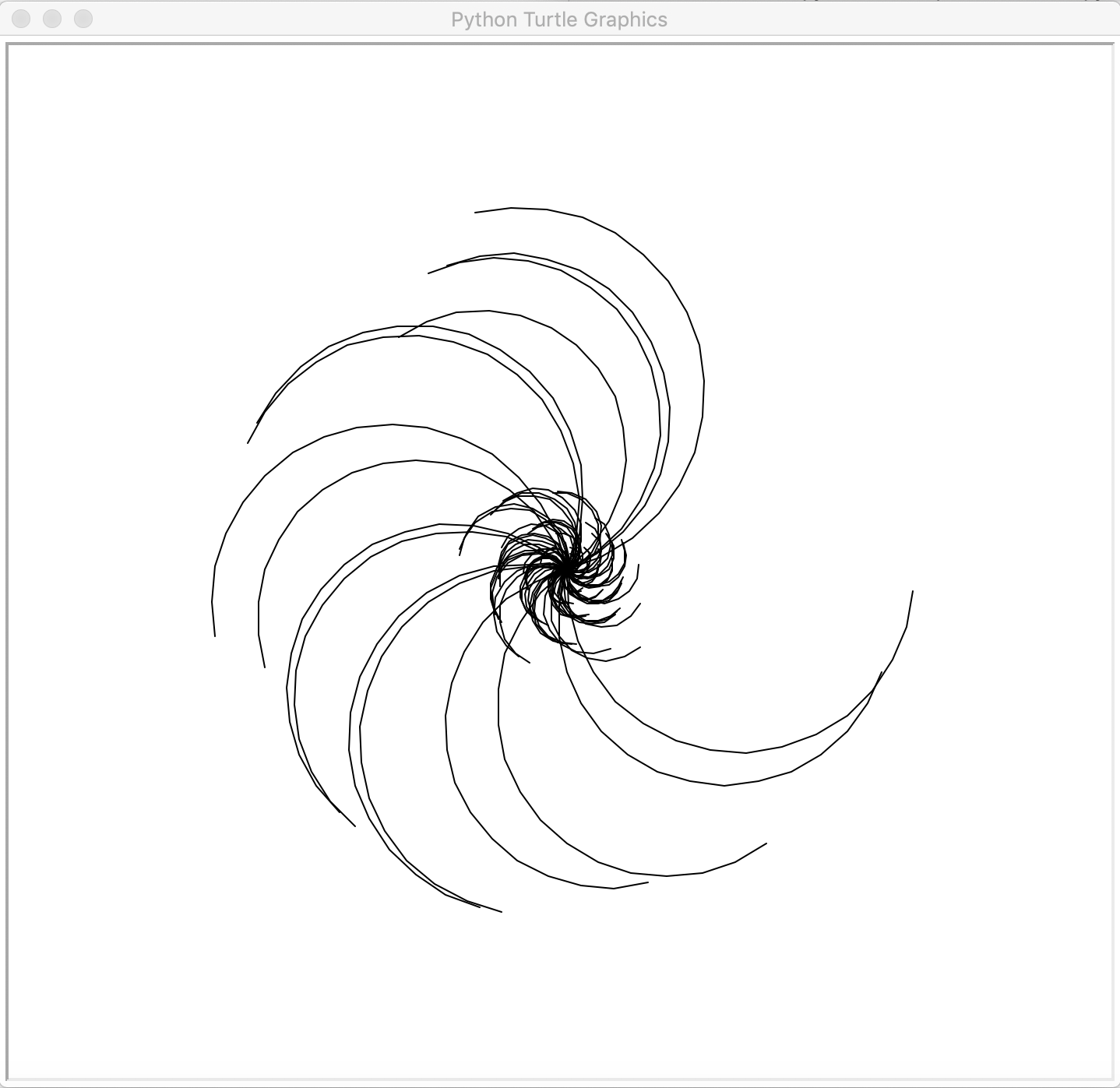
Steps to reach one in hailstone sequence as radii of half circles for integers 1-100
💻 Add a random color element to the visualization
You will need to reference the following: